序
浏览学长博客有感,稍微记一点:
1.正则化损失函数L2
2.学习率的指数衰减
3.滑动平均模型
ps:看到类似的
博客
也不错
正则化损失函数L2
概念简述:
由于数据存在很多干扰或者噪声,容易产生过拟合现象。在相同网络结构下,决策面越复杂,参数w的值往往更大,而w较小时候,得到的决策面相对平缓。
L2正则化是一种减少过拟合的方法,让w尽量小,在损失函数中加入刻画模型复杂程度的指标。假设损失函数是J(θ),则优化的是J(θ)+λR(w),R(w)=∑ni=0|w2i|。
公式推导
正则化函数理解(比较好)
代码实现
training.py中:
#正则化损失函数L2
REGULARATION_RATE = 0.0001
regularizer =tf.contrib.layers.l2_regularizer(REGULARATION_RATE)
model.py中
# fc1密集全连层中,将权重的正则化结果加入损失集合“loss”
with tf.variable_scope("fc1") as scope:
W_fc1 = weight_variable([6 * 96, 256]) # 输入维度为1*6*96,输出维度为256
if regularizer != None:
tf.add_to_collection('loss', regularizer(W_fc1))
b_fc1 = bias_variable([256])
fc1 = tf.nn.relu(tf.matmul(h_pool5_flat, W_fc1) + b_fc1, name="fc1")
#fc2可以同理
然后再在training.py中
loss1 = cross_entropy_mean + tf.add_n(tf.get_collection('loss'))
即用交叉熵损失和权重损失之和,代替原来的交叉熵损失
学习率的指数衰减
概念简述:
使用固定的 α,不能精确的收敛,算法最后在附近摆动,所以采用指数衰减
这里使用退化学习率,公式为:
decayed_learning_rate = learning_rate * decay_rate ^ (global_step / decay_steps)
对应函数为
tf.train.exponential_decay(learning_rate, global_step, decay_steps, decay_rate, staircase=False, name=None)
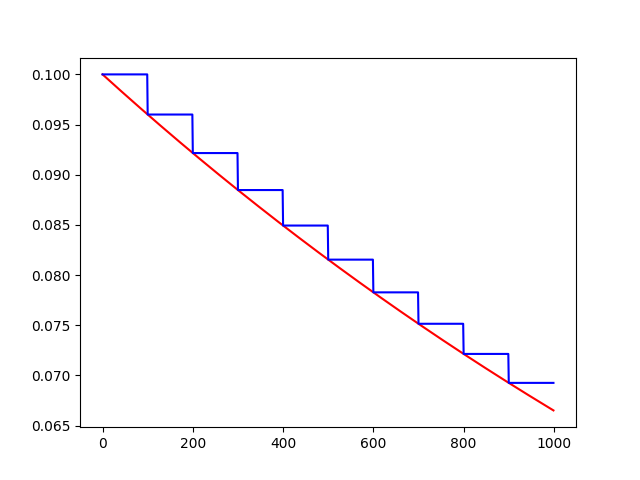
摘自博客,不理解建议看原博
代码实现
在training.py里
LEARNING_RATE_BASE = 0.8
LEARNING_RATE_DECAY = 0.99
BATCH_SIZE = 128
global_step = tf.Variable(0, trainable=False)
#设置指数衰减的学习率
learning_rate = tf.train.exponential_decay(
LEARNING_RATE_BASE,
global_step,
100000 / BATCH_SIZE,
LEARNING_RATE_DECAY
)
在model.py中
#往梯度下降优化器里传入参数学习率(我封装在函数里了)
def trainning(loss,learning_rate):
# 梯度下降
train_step = tf.train.AdamOptimizer(learning_rate).minimize(loss)
return train_step
training.py中调用
train_step = model.trainning(loss1,learning_rate)
### 滑动平均模型
**概念简述**:tf.train.ExponentialMovingAverage实现滑动平均模型,提高模型在测试数据上的健壮性。 > 说白了就是在更新参数的时候不太过了也不太小,更新参数跟你之前的参数有联系,不会发生突变。健壮性就是对突变的抵抗能力,健壮性越好,这个模型对恶性参数的提抗能力就越强。你训练的时候万一遇到个“疯狂”的参数,有了这个算法疯狂的参数就会被抑制下来,回到正常的队伍里 ExponentialMovingAverage对每一个待更新的变量(variable)都会维护一个影子变量(shadow variable)。影子变量的初始值就是这个变量的初始值, > shadow_variable=decay×shadow_variable+(1−decay)×variable ExponentialMovingAverage 还提供了 num_updates 参数来动态设置 decay 的大小: > decay=min{decay,1+num_updates10+num_updates} [实例](https://blog.csdn.net/IAMoldpan/article/details/78208897?locationNum=11&fps=1)
ps:一开始0.99和计算后的0.1相比取0.1,之后计算结果0.99较小取0.99 **代码实现**
#tf.trainable_variables返回的是需要训练的变量列表
在training.py中
# 定义损失函数、学习率、滑动平均操作以及训练过程
variable_averages = tf.train.ExponentialMovingAverage(
MOVING_AVERAGE_DECAY, global_step)
variable_averages_op = variable_averages.apply(
tf.trainable_variables())
#训练与更新参数的滑动平均值
#将2大步操作打包在train_op中,第1大步操作是使用正则化和指数衰减更新参数值
#第2大步操作是使用滑动平均再次更新参数值。
#每次训练都完成这2大步操作。
with tf.control_dependencies([train_step, variable_averages_op]):
train_op = tf.no_op(name='train')
#然后在训练的时候调用train_op就完事拉
总结:
- 正则化:防止过拟合
- 学习率衰减: 最优值收敛
- 滑动均值模型: 抵御突变数据,增强模型健壮性
- 最后完整代码见序中两篇博客···
=====================================================2018.8.31